This page is located at: http://www.ncsall.net/?id=316
Seeing is Believing
by Charles Brover, Denise Deagan, and Solange Farina
MEG has often returned to the problem of teaching signed integers and the
difficulties associated with learning the multiplication of negative numbers.
Students in pre-GED and GED classes are often "given" the rules for the
operations of signed integers, which they dutifully try to commit to memory.
However, without understanding the mathematics involved in the operations of
signed numbers, this memorization feat usually fails them.
In MEG's workshop, teachers conduct an investigation, visualizing and
analyzing the problems of signed integers with the aid of manipulatives:
two-color counters (small chips with a different color on each side).
We typically begin the investigation using the counters to model the operations of addition and subtraction of signed integers. We investigate whether a yellow (positive) chip and a red (negative) chip equal zero, using the two-color counters. We confirm that each pairing of a yellow chip (+1) and a red chip (-1) resulted in the value of 0. Thus we visualize the mathematical concept of the additive inverse.
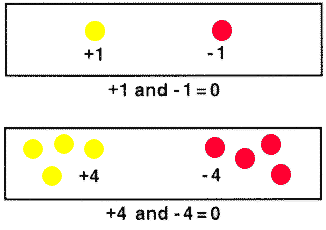
It could then follow that one could add or remove pairs of yellow and red chips to and from the grid - each pair representing a sum of 0 - without affecting the total value of the amount remaining.

The original value of the above was 0. If one removes a red and a yellow chip (a "0" value pair) the value remains zero.
This application of zero-sum pairs can be extended to create a visual version of any addition or subtraction problem.

To find the value represented in the preceding box, you can remove 0-value red and yellow chip pairs until only one color remains.
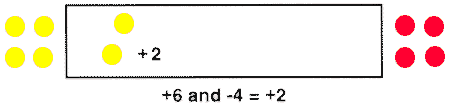
Thus, we are able to visualize the operation of addition with signed integers as we add or remove positive or negative chips.
After modeling a variety of subtraction and addition problems, we tackle multiplication. Each group in the workshop is asked to place a 0-value set of counters in front of them. For example,
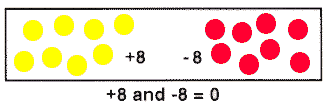
The groups are then asked to model multiplication of two negative integers, for instance, "- 3(-2)" by removing -2 three times.
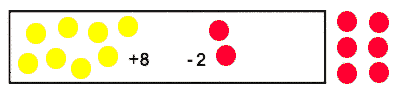
Applying knowledge of addition and subtraction we can see why the solution is +6.
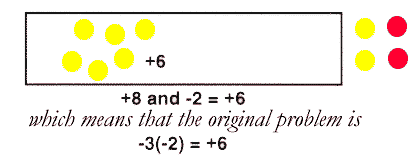
The idea that the multiplication of negative numbers yields a positive number can be daunting for many students, suggesting a general "irrationality" in math. "Just give me the rule," say some students out of frustration. This is all the more reason to provide students with opportunities to wrestle with the problem.
******************
Along with the manipulative model using two-color counters, MEG workshops also explore a variety of explanatory models. For example, we examine the pattern created with the multiplication of negative numbers:
3(-2) = -6
2(-2) = -4
1(-2) = -2
0(-2) = 0
As we increase the multiplier by one, the product is increased by two. So, for the pattern to continue, the multiplier must become a negative number:
-1(-2) = 2
-2(-2)
= 4
Another explanatory model demonstrates that multiplying two negative numbers results in a positive number because mathematical logic requires negative integers to follow the same rules as positive integers. This leads to a consideration of the distributive property:
a (b + c) = ab + ac
If we assign values a = - 2, b = 3, c = - 3 then
-2(3 + (-3)) = (-2)(3) + (-2)(-3)
where - 3 is the additive inverse of 3, so added together they equal 0.
-2(0) = (-6) + (6)
0 = 0>
The explanatory power of this model derives from the logical consideration of the equation. If one does not accept that (-2)(-3) yields a positive, then it must yield a negative, which would produce the self-evidently false 0 = (-12).
******************
In addition to the math content, the investigation of signed numbers is informed by the history of mathematics. Students who may be having difficulty with signed number concepts are delighted to discover that for centuries this constellation of problems has intrigued and sometimes confounded mathematicians. The Chinese reportedly used colored rods for the calculation of negative numbers as early as 500 BCE, and Brahmagupta, a 7th century CE mathematician from India, explicitly used negative numbers, as well as zero, in his algebraic work. In the 1500s, however, many European mathematicians argued against the existence of negative numbers, by stating that zero signifies nothing, and it is impossible for anything to be less than nothing (Brown, 1999). Giancarlo Cardano, an Italian mathematician of the 16th century, wrote about negative numbers and called them "false numbers." It was not until the 18th century that the mathematician Leonard Euler proved that the product of (-1)(-1) had to be either 1 or -1, and that since it was already established that (1)(-1) = -1, then (-1)(-1) = 1 (Billstein, Libeskind, & Lott,1990).
At each MEG meeting we save time for writing and reflection. Writing in journals helps teachers to integrate the basic arithmetic they are teaching with the deeper mathematical content they are learning. After the meeting on signed numbers, one teacher wrote, "To understand mathematics is to understand the beauty of its symmetry, its aesthetic, its patterns. Using manipulatives of all kinds just serves to bring one closer to that appreciation. To "get it" somehow. Not by rote but through exploration. And fun, ultimately. To engage as one would in a great story. The story of mathematics is as vibrant as the story of English. But much less often told."
Another teacher connected his experience with the two-color counter activity to his classroom practice: "Interesting modeling of + -, where +- equals 0. Will possibly intrigue students and give an explanation of positive/negatives: adding, subtracting, multiplying (I'd like to see dividing!), which could lead one to accept and absorb the rules more readily. It reminds me of knowing the concept of multiplying, (e.g., four groups of 5, arriving at 20). Many of my students do multiplying through addition. [But] there is no substitute for knowing the rules. It's great to demystify the processes, [to] give a general feel so that the rules are connected."
Some teachers who have attended MEG workshops initiate similar activities with two-color counters in their classrooms. They allow their students to develop conjectures and rules for operations with signed numbers based on students' hands-on experience and understanding of the underlying math concepts. Instead of responding to abstract and sterile injunctions to have their students memorize standard algorithms, these teachers see that their students can learn the mathematics and construct the rules simultaneously. And seeing then really is believing.
For more information on this activity, consult the NCTM's Algebra for Everyone video (available from NCTM at ( 703) 620-9840 for $47.50).
References
Billstein, R., Libeskind, S., & Lott, J. (1990) A Problem Solving Approach to Mathematics for Elementary School Teachers, Fourth Edition. Redwood City, CA: Benjamin/Cummings Publishing Company.
Brown, K.S. (1999) The History of Mathematics (MathPages).www.seanet.com/ksbrown/kmath298.html
